Bresler–Pister yield criterion

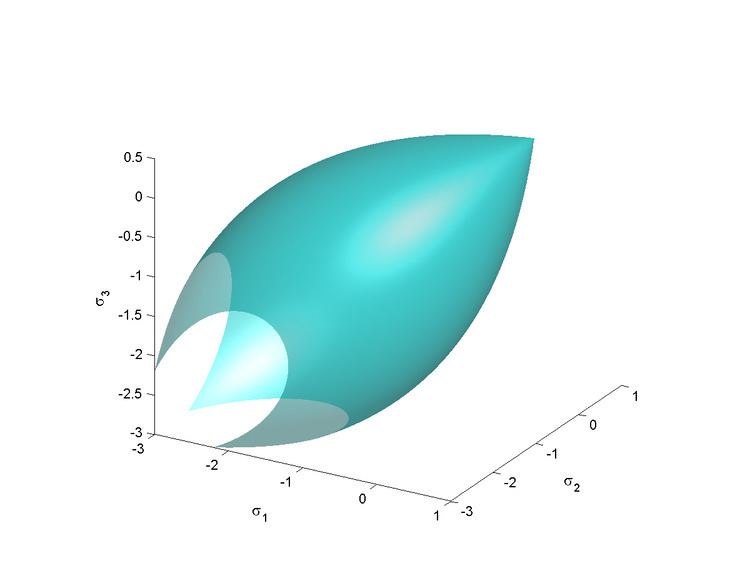
The Bresler–Pister yield criterion is a function that was originally devised to predict the strength of concrete under multiaxial stress states. This yield criterion is an extension of the Drucker–Prager yield criterion and can be expressed on terms of the stress invariants as

${\displaystyle {\sqrt {J_{2}}}=A B~I_{1} C~I_{1}^{2}}$

where ${\displaystyle I_{1}}$ is the first invariant of the Cauchy stress, ${\displaystyle J_{2}}$ is the second invariant of the deviatoric part of the Cauchy stress, and ${\displaystyle A,B,C}$ are material constants.

Yield criteria of this form have also been used for polypropylene and polymeric foams.

The parameters ${\displaystyle A,B,C}$ have to be chosen with care for reasonably shaped yield surfaces. If ${\displaystyle \sigma _{c}}$ is the yield stress in uniaxial compression, ${\displaystyle \sigma _{t}}$ is the yield stress in uniaxial tension, and ${\displaystyle \sigma _{b}}$ is the yield stress in biaxial compression, the parameters can be expressed as

${\displaystyle {\begin{aligned}B=&\left({\cfrac {\sigma _{t}-\sigma _{c}}{{\sqrt {3}}(\sigma _{t} \sigma _{c})}}\right)\left({\cfrac {4\sigma _{b}^{2}-\sigma _{b}(\sigma _{c} \sigma _{t}) \sigma _{c}\sigma _{t}}{4\sigma _{b}^{2} 2\sigma _{b}(\sigma _{t}-\sigma _{c})-\sigma _{c}\sigma _{t}}}\right)\\C=&\left({\cfrac {1}{{\sqrt {3}}(\sigma _{t} \sigma _{c})}}\right)\left({\cfrac {\sigma _{b}(3\sigma _{t}-\sigma _{c})-2\sigma _{c}\sigma _{t}}{4\sigma _{b}^{2} 2\sigma _{b}(\sigma _{t}-\sigma _{c})-\sigma _{c}\sigma _{t}}}\right)\\A=&{\cfrac {\sigma _{c}}{\sqrt {3}}} B\sigma _{c}-C\sigma _{c}^{2}\end{aligned}}}$

Alternative forms of the Bresler-Pister yield criterion

In terms of the equivalent stress (${\displaystyle \sigma _{e}}$) and the mean stress (${\displaystyle \sigma _{m}}$), the Bresler–Pister yield criterion can be written as

${\displaystyle \sigma _{e}=a b~\sigma _{m} c~\sigma _{m}^{2}~;~~\sigma _{e}={\sqrt {3J_{2}}}~,~~\sigma _{m}=I_{1}/3~.}$

The Etse-Willam form of the Bresler–Pister yield criterion for concrete can be expressed as

${\displaystyle {\sqrt {J_{2}}}={\cfrac {1}{\sqrt {3}}}~I_{1}-{\cfrac {1}{2{\sqrt {3}}}}~\left({\cfrac {\sigma _{t}}{\sigma _{c}^{2}-\sigma _{t}^{2}}}\right)~I_{1}^{2}}$

where ${\displaystyle \sigma _{c}}$ is the yield stress in uniaxial compression and ${\displaystyle \sigma _{t}}$ is the yield stress in uniaxial tension.

The GAZT yield criterion for plastic collapse of foams also has a form similar to the Bresler–Pister yield criterion and can be expressed as

${\displaystyle {\sqrt {J_{2}}}={\begin{cases}{\cfrac {1}{\sqrt {3}}}~\sigma _{t}-0.03{\sqrt {3}}{\cfrac {\rho }{\rho _{m}~\sigma _{t}}}~I_{1}^{2}\\-{\cfrac {1}{\sqrt {3}}}~\sigma _{c} 0.03{\sqrt {3}}{\cfrac {\rho }{\rho _{m}~\sigma _{c}}}~I_{1}^{2}\end{cases}}}$

where ${\displaystyle \rho }$ is the density of the foam and ${\displaystyle \rho _{m}}$ is the density of the matrix material.

References

See also

• Yield surface
• Yield (engineering)
• Plasticity (physics)